Chapitre 4: les paramètres de dispersion
Nous avons vu que les valeurs centrales sont
nécessaires pour caractériser une série statistique, cependant elles ne sont
pas en général suffisantes pour donner une conclusion sur la répartition d’un
caractère, ainsi par exemple on peut rencontrer deux populations ayant même
valeur centrale mais elles n’ont pas une même dispersion autour du centre.
Soit par exemple les notes de deux
étudiants dans cinq matières :
|
|
L’étudiant N° 1
|
L’étudiant N° 2
|
|
Philosophie
|
6
|
2
|
|
Histoire
|
8
|
6
|
|
Mathématiques
|
10
|
10
|
|
Anglais
|
12
|
14
|
|
Français
|
14
|
18
|
Les deux étudiants ont même moyenne et même
médiane : 10, mais nous remarquons que leurs notes ne sont pas réparties
de la même façon autour de la valeur central. On dit donc que les deux séries n’ont pas la même répartition,
et plus précisément la série 2 (notes de l’étudiant N° 2) est plus dispersée
que la série 1 (note de l’étudiant N° 1).
1- L’étendue de la série :
L’étendue, appelée aussi amplitude ou intervalle
maximale d’une série est égale à la différence des valeurs extrêmes de la série.
Elle est notée E; Ainsi dans l’exemple précédent des notes des deux étudiants
N°1 et N°2 la série {6, 8, 10, 12, 14} a pour étendue E = 14 – 6 = 8. Et la série {2, 6, 10, 14, 18} a pour étendue E = 18 – 2 = 16.
2- Les quantiles :
Définition :
|
|
Autrement
dit un quantile d’ordre n est une série ayant n groupes d’effectifs égaux.
Ainsi la médiane est un quantile d’ordre 2.
Les quantiles les plus fréquemment
utilisées dans la statistique descriptive sont :
-La
médiane Me : est le quantile d’ordre 50%. Elle partage la série des
valeurs observées en deux séries de même taille.
-Les
quartiles, c’est-à-dire les quantiles d’ordre 4, notée Q1, Q2,
Q3, elle partage la série en 4 séries de même taille :
25%
des observations sont inférieures au 1er quartile Q25 :
50%
des observations sont inférieures au 2ème quartile Q50 :
75%
des observations sont inférieures au 3ème quartile Q75 :
-Les déciles ; ce sont
les quartiles d’ordre 10, ils partagent l’effectif total en dix groupes égaux.
Il y en a neuf déciles notés D1, D2, D3……..D9.
-Les centiles ; ce sont
les quartiles d’ordre 1, ils partagent l’effectif total en quatre-vingt-dix
groupes égaux. Elles sont notées C1, C2, C3……..C99.
3-Les intervalles
interquantiles :
La différence Q75
– Q25 s’appelle écart interquartile.
L’intervalle interdécile noté ID ou I.Id est la
différence entre Q90 et Q10, et on a :
ID = Q90
– Q10, cet intervalle contient 80% des observations.
La différence Q90 – Q10 s’appelle
écart interdécile.
L’intervalle interdécile noté IC ou I.IC
est la différence entre Q99 et Q1, et on a :
IC = Q99
– Q1, cet intervalle contient 98% des observations.
La
différence Q99 – Q1 s’appelle écart intercentile.
Tous ces écarts permettent de mesurer la dispersion de
la série autour de la médiane.
Exemple :
On donne la distribution
des revenus annuels des 460 cadres d’un groupe bancaire
|
Classe de revenus (en dirhams)
|
Effectifs
|
|
de 50 000 à moins de 70 000
de 70 000 à moins de 80 000
de 80 000 à moins de 90 000
de 90 000 à moins de 100 000
de 100 000 à moins de 105 000
de 105 000 à moins de 110 000
de 110 000 à moins de 120 000
de 120 000 à moins de 130 000
de 130 000 à moins de 140 000
de 140 000 à moins de 160 000
de 160 000 à moins de 190 000
|
24
32
51
70
47
41
70
58
40
24
3
|
Déterminer l’étendre de la série, et les intervalles
interquartile et interdécile.
En effet
|
Classe de revenus
(en milliers de dirhams)
|
Effectifs
|
Effectifs cumulés croissants ‘ECC’
|
|
[ 50 , 70 [
[ 70 , 80 [
[ 80 , 90 [
[ 90 , 100 [
[ 100 , 105 [
[ 105 , 110 [
[ 110 , 120 [
[ 120 , 130 [
[ 130 , 140 [
[ 140 , 160 [
[160 , 190 [
|
24
32
51
70
47
41
70
58
40
24
3
|
24
56
107
177
224
265
335
393
433
457
460
|
L’étendue de la série est E = 190 – 50 = 140 milliers
de dirhams.
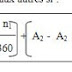
Le quartile Q1 correspond au caractère du 460/4 = 115ième
individu. Il appartient à la classe 90 – 100 :=
Le quartile Q3 correspond au caractère du
(3/4) x 460 = 345ième individu. Il appartient à la classe 110 –
120 :=
L’intervalle interquartile
est IQ = Q75 – Q25
= 121,72 – 95,6 = 26,12.
Soit 26 120 DH.
Le décile D1 correspond au caractère du 460/10 =
46ième individu. Il appartient à la classe 70 – 80 :
De même Le décile D9
correspond au caractère du 9 x 460/10 = 414ième individu. Il
appartient à la classe 70 – 80 :130 + 10 X 21/40=135,525
L’intervalle interdécile est
Id = D9 – D1 = 135,525 – 76,975 = 58,55
Soit
58 550 DH.
4- L’écart absolu
moyen :
4-1- Ecart absolu moyen
par rapport à la moyenne :
L’écart
absolu moyen par rapport à la moyenne noté ec, encore appelé écart arithmétique, est la moyenne
arithmétique des valeurs absolues des écarts de tous les termes de la série à
leur moyenne arithmétique
Remarquons
que cet écart absolu moyen est nul si les observations sont égales.
4-2- Ecart absolu moyen
par rapport à la médiane :
L’écart absolu moyen par rapport à la
médiane noté eMe, est la moyenne arithmétique des valeurs absolues
des écarts de tous les termes de la série à leur médiane.
Exemple :
On considère la distribution suivante :
a) calculer l’écart absolu
moyen par rapport à la moyenne.
b) calculer l’écart absolu
moyen par rapport à la médiane.
En
effet,
a) X= 45,6 eX= 11,75
b) Me = 45 + 10.(50 – 46)/29 » 46,38 et eMe » 11,69.
5- Variance et écart-type
Les paramètres de dispersion sont des
nombres qui mesurent la dispersion des valeurs autour d’un paramètre de
position (c, Me, …). Ils s’expriment
dans la même unité que les observations et permettent de comparer des séries
statistiques de même nature.
5-1- Variance :
Variance d’une série non
pondérée
5-2- Ecart- type :
On appelle écart-type la racine carrée de la variance. On
note
Ecart-type d’une série
pondérée
Le calcul de l’écart-type pour les
séries pondérées n’est pas fondamentalement différent de celui effectué
précédemment : les écarts à la moyenne doivent être comptés autant de fois
qu’ils apparaissent dans la série.
Si la série est à caractère continu,
comme pour le calcul de moyenne, on prend pour valeur du caractère le centre de chaque classe.
6- Coefficient de
variation :
Pour faciliter les comparaisons entre
séries, on utilise une mesure de dispersion relative appelée coefficient de
variation.
Cv= s / c
|
Chapitre 4: les paramètres de dispersion
 Reviewed by IstaOfppt
on
06:05
Rating:
Reviewed by IstaOfppt
on
06:05
Rating:
 Reviewed by IstaOfppt
on
06:05
Rating:
Reviewed by IstaOfppt
on
06:05
Rating:













Aucun commentaire: