Calculs commerciaux TP
I- rapports et
proportions
1- Rapport
Le rapport d’un nombre (a) à un autre nombre (b) est le quotient (K) de ces deux nombres
|
/
Exemples
32
·
 Le
rapport de 32 à 8 est :
= 4
Le
rapport de 32 à 8 est :
= 4
8
13
·
 Le
rapport de 13 à 2 est : / = 6,5
Le
rapport de 13 à 2 est : / = 6,5
2
2- Proportion
La proportion est l’égalité formée de deux rapports
a
c
/ = /
b d
|
Exemples
4 16
7
28
Dans la
proportion a = c , les
nombres : - a et b sont appelés les extrêmes
/ b /d - b et
c sont appelés les moyens
3- Propriétés des
proportions
Lorsqu’on dispose d’une proportion, on peut effectuer
différentes transformations.
3- 1- Dans toute proportion, le produit des extrêmes
est égal au produit des moyens.
|
a/b = c/d
a x d = c x b
3-2-
Disposant de quatre nombres tels que
le produit de deux d’entre eux est égal au produit des deux autres, on conclut
que ces quatre nombres forment une proportion, soit quatre nombres a, b, c et d
tels que :
a x d = b x c
Divisons tout d’abord les
deux membres de l’égalité par b :
Après simplification du
premier membre de l’égalité, on obtient :
a c
/ = /
b d
|
3-4- Si deux rapports forment une proportion, on obtient
un rapport égal aux deux premiers en prenant pour numérateur la somme
des numérateurs et pour dénominateur la somme des dénominateurs.
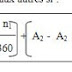
3-5- On obtient aussi un rapport égal si on utilise la différence.
a c a - c
/ = / =
/
b d b - d
3-6- ax cy ax + cy
/ = / =
/
bx dy bx + dy
4- Suite de rapports égaux
Disposant de plusieurs rapports égaux, on
peut former une suite de ces rapports égaux.
a c e
b d f
On peut former une suite
ayant la forme suivante :
a c e
/ = / =
/
b d f
5- Propriétés des suites
de rapports égaux
Elles
ont les mêmes propriétés que les proportions.
a c e a + c+ e
/ = / = / = /
b d f b + d + f
et on peut les écrire sous la
forme suivante :
a c e ax+ cy+ ez
/ = / =
/ = /
b d f bx + dy + fz
II- Grandeurs
proportionnelles
1- Grandeurs directement
proportionnelles
1-1- Exemple
Soit le tableau
ci-après :
Salaire encaissé
|
Nombre d’heures de travail
|
Rapport (taux horaire)
|
||
1 050 DH
1 700 DH
2 350 DH
2 550 DH
3 100 DH
………………
A DH
|
42 heures
68 heures
94 heures
102 heures
124 heures
……………..
B heures
|
1
050 = 25
42
1 700
= 25
68
2
350 = 25
94
2
550 = 25
102
3
100 = 25
124
……………..
A
= K(25)
B
|
1-2- Constatation
- le rapport de chaque
salaire à la durée correspondante est constant (25) ;
- ces valeurs forment une
suite de nombres directement proportionnels.
1-3- Conclusion
On dit que les « salaires »
et les « durées » correspondantes sont deux grandeurs directement
proportionnelles.
1-4- Définition
Deux grandeurs qui varient
simultanément sont directement proportionnelles quand le rapport des mesures
correspondantes est constant.
Exemple de grandeurs directement proportionnelles
- prix d’une
marchandise et son poids;
- salaire d’un ouvrier
(payé à la pièce) et nombre de pièces fabriquées;
- prime d’ancienneté
encaissée par un ouvrier et nombre
d’années de travail ; etc.
Les grandeurs a, b,
et c
sont proportionnelles à A,
B, et C
a b c
A B C
Exemple
Les grandeurs : 14,
24, et 30
sont proportionnelles à :
42,
72, et 90
14
24 30
42
72 90
1-5- Propriétés
1- Soient a et b deux mesures de grandeurs directement
proportionnelles et K la valeur du rapport constant appelé COEFFICIENT DE
PROPORTIONNALITE.
a
b
Lorsque deux grandeurs sont
directement proportionnelles, la mesure de l’une est égale au produit de la
mesure correspondante de l’autre par le coefficient de proportionnalité.
2- Soient (y1, x1) et (y2,
x2) deux couples de mesures correspondantes de deux grandeurs
proportionnelles, de la définition, il découle :
y1 y2 y1 x1
Lorsque
deux grandeurs sont directement proportionnelles, le rapport de deux mesures
quelconques de l’une est égal au rapport de deux mesures correspondantes de
l’autre.
Du tableau du B-1. 1er paragraphe, on vérifie
que :
2 350 94
1 700 68
3-
Soient y et x un couple de mesures
correspondantes de deux grandeurs directement proportionnelles, il
découle :
Lorsque
deux grandeurs sont directement proportionnelles, si la mesure de l’une est
multipliée (ou divisée) par un nombre quelconque, la mesure correspondante de
l’autre est multipliée (ou divisée) par le même nombre.
Du
tableau du B – 1. 1er paragraphe, on vérifie qu’au couple (1
700 ; 68) correspondant le couple (2 550 ; 1 02).
1 700
68
x 1,5 x
1,5
2
550 102
2- Grandeurs inversement
proportionnelles
2-1- Exemple
Le tableau suivant donne le nombre d’articles (de prix
unitaires variables) qu’on peut acquérir avec 10 000 DH.
2-2 Constatation
- le produit des couples de
mesures correspondantes est constant (10 000) ;
- ces mesures forment une
suite de nombres inversement proportionnels.
2-3 Conclusion
On dit que le nombre d’articles achetés
et le prix unitaire correspondant sont deux grandeurs inversement
proportionnelles.
2-4- Définition
Deux grandeurs qui varient
simultanément sont inversement proportionnelles quand le produit de
leurs mesures correspondantes est constant.
Exemple de grandeurs inversement proportionnelles
- la durée d’un trajet et la
vitesse ;
- pour un travail donné, le
nombre d’ouvrier et le temps à passer pour l’exécuter…, en supposant une durée
de travail uniforme pour chaque ouvrier.
2-5- Propriétés
1- Soient y et x deux mesures de grandeurs inversement
proportionnelles et K le produit constant ;
y
1
x
Lorsque deux grandeurs sont inversement
proportionnelles, les mesures de l’une d’elles sont directement
proportionnelles aux inverses des mesures correspondantes de l’autre.
250 200
125 100
1 1 1 1
40 50 80 100
40 50
1 1
80 100
1
1
2- Soient (y1, x1) et (y2,
x2) deux couples de mesures correspondantes de deux grandeurs inversement
proportionnelles :
y1 × x1 = y2
× x2 = K
ou y1 = y2
= K
x1 x2
1
y1 x1
y2 1
x2
y1 x2
y2 x1
Lorsque
deux grandeurs sont inversement proportionnelles, le rapport de deux mesures
quelconques de l’une est égal au rapport inverse de deux mesures correspondantes
de l’autre.
250 50
200 40
200 x 50 = 10 000.
3- Soit y et x un couple de grandeurs inversement
proportionnelles.
y y × m y × m
1 1 m
x
m
Lorsque
deux grandeurs sont inversement proportionnelles, si la mesure de l’une est
MULTIPLIEE (ou divisée) par un nombre quelconque, la mesure de l’autre est DIVISEE (ou multipliée) par ce
nombre.
3- Grandeurs directement
proportionnelles à plusieurs autres
3-1
Exemple
Le tableau suivant donne le prix d’un terrain en
fonction de ses dimensions (longueur et largeur).
On constate que :
-
le prix est directement proportionnel à la longueur et aussi à la
largeur ;
-
le rapport du prix au produit des mesures correspondantes des longueur et
largeur est constant.
3-2- Définition
Une grandeur est
directement proportionnelle à plusieurs autres si elle est directement
proportionnelle à chacune d’elles
3-3-
Propriétés
1-
Lorsqu’une grandeur est directement
proportionnelle à plusieurs autres, le rapport d’une mesure quelconque de cette
première grandeur au produit des mesures correspondantes des autres est
constant (voir tableau, 4e colonne).
2-
Une mesure quelconque d’une grandeur
proportionnelle à plusieurs autres est égale au produit des mesures
correspondantes des grandeurs auxquelles elle est proportionnelle par le
coefficient de proportionnalité.
P
x × y
III – Partages
proportionnels
1 – Grandes directement
proportionnelles
1-1- Définition
Partager un nombre N proportionnellement aux nombres
donnés a, b et c, c’est déterminer les nombres x, y et z tels que l’ont ait la
suite des rapports égaux :
x y z
a b c
1-2- Calcul de x, y et z
Nous proposons une solution simple. Posons une suite de
rapports égaux.
x y z
x + y + z N
a
b c a + b + c
a + b + c
x
a
y
b
z
x + y + z = aK + bK + cK
x + y + z = K(a + b + c)
x + y+ z N
a + b + c a + b + c
En remplaçant K par sa valeur dans les expressions
(1), (2) et (3), nous trouvons les valeurs de x, y et z.
2-
Grandeurs inversement proportionnelles
§ définition
Partager
un nombre N inversement proportionnellement aux nombres données a, b et c,
c’est déterminer les nombres x, y et z tels que l’on ait la suite des rapports
égaux :
x y z
1 1 1
a b c
N.B : ce problème revient en quelque sorte à
partager un nombre aux inverses des nombres donnés.
APPLICATIONS
§ Application 1
Partager 80 000 DH proportionnellement à 5, 4 et 11.
-
Solution
Soient
x, y et z les trois nombres demandés.
x
y z
5
4 11
x
5
y
4
z
x + y + z
= 20 K
80 000
20
K = 4 000
d’où : x =
5 x 4 000 = 20 000 DH
y
= 4 x 4 000 = 16 000 DH
z = 11
x 4 000 = 44 000 DH
-
Vérification : 80 000
DH.
§ Application 2
Partager 15 300 DH inversement proportionnellement aux
nombres 3, 4 et 8.
-
Solution
Soient
x, y et z les nombres demandés ; on a :
x y
z
1 1
1
3 4 8
1
1 1
3 4 8
D.C.
= 24
1
1 x 8 8 1 1 x 6
6 1 1 x 3
3
3 3 x 8 24
4 4 x 6 24
8 8 x 3
24
1 1 1
8 6 3
3 4 8
8 6
3
24 24
24
x y z x y z
1 1
1 8 6 3
3 4 8 24 24
24
x y z
8 6 3
x
8
y
6
z
x + y +
z = 17 K
x + y + z 15 300
17 17
Remplaçant
K par sa valeur.
x
= 8 x 900 = 7 200 DH
y
= 6 x 900 = 5 400 DH
z
= 3 x 900 = 2 700 DH
Vérification : 15 300 DH.
|
Calculs commerciaux TP
 Reviewed by IstaOfppt
on
12:48
Rating:
Reviewed by IstaOfppt
on
12:48
Rating:
 Reviewed by IstaOfppt
on
12:48
Rating:
Reviewed by IstaOfppt
on
12:48
Rating:








Aucun commentaire: