Mathématiques financièresTCEII

Exercice 1 :

            Une dette de 400 000 dh est remboursable par le versement de 12 annuités  de 66 000 dh.

Travail à faire :

            Sachant que le premier versement a lieu u an après la date du contrat, calculer le taux d’escompte. Quel aurait été le taux si le premier versement avait eu lieu deux ans après la date du contrat ?

Exercice 2 :

            Quelle somme constante doit-on verser à la fin de chaque mois pendant 4 ans, pour rembourser une dette de 180 000 dh, contractée un mois avant le 1^er versement ? Taux : 13%. Donner deux solutions.

Exercice 3 :

            Un particulier a contracté auprès d’une banque un emprunt de montant D. Cet emprunt est remboursable par trimestrialités constantes de 9 000 dh chacune et ceci pendant 6 ans.

Travail à faire :

            Sachant que le 1^er versement est payable un an après la date du contrat, calculer le nominal D de la dette. Taux : 12,5 % l’an, (utiliser les taux proportionnels).

Exercice 4 :

            Un organisme financier accorde des crédits-logement dans les conditions suivantes :

-         taux annuel : 12,5 %.

-         remboursement sur 15 ans par mensualités constantes, la première étant payable 1 mois après la date du contrat (on utilise alors les taux proportionnels).

-         la mensualité ne doit pas dépasser les 30 % du revenu mensuel du ménage.

Travail à faire :

1-     Calculer le montant maximum qui peut être accordé à un ménage dont le revenu mensuel est de 12 000 dh par mois.

2-     En cas de remboursement par anticipation les mensualités non échues sont actualisées à 10 % l’an.

* Calculer le montant que doit verser un ménage, pour se libérer de sa dette, juste après le paiement de la 84^ème mensualité, et ayant bénéficié d’un crédit de 200 000 dh. (Utiliser les taux proportionnels).

* Expliquer pourquoi le taux est diminué.

Réponses:

Solution :

Exercice 1 :

         1^er cas :

                                      400 000 = 66 000 1 – (1 + i)^-12

                                                                     i

         par tâtonnement (ou par la table n 4) puis par interpolation linéaire on trouve un taux de 12,47% l’an.

         2^ème cas :

                                      400 000 = 66 000 1 – (1 + i)^-12  (1 +i)^-1

                                                                     i

         par tâtonnement puis par interpolation linéaire on trouve un taux de 10,38%.

Exercice 2 :

         1^ère solution : utilisation des taux proportionnels.

                                      i =  0,13 = 0,108333

                                           12

                                      a 1 – 1,0108333^-48 = 180 000 → a = 4 828,95

                                                    i

         2^ème solution : utilisation des taux équivalents.

                                      i =  1,13^1/12 – 1  = 0,0102368

                                      a 1 – 1,0102368^-48 = 180 000 → a = 4 765,25

                                          0,0102368

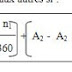
Exercice 3 :

         Ici on a un différé de 9 mois :

                            D = 9 000 1 – 1,03125^-24 x 1,03125^-3 = 137 126,15 dh

                                              0,03125

Exercice 4 :

a)    : La capacité de remboursement du ménage est de

             12 000 x 0,3 = 3 600 dh par mois

D’où le montant demandé :

              D = 3 600 1 – 1,010416666^-180 = 292 084,02 dh

                                 0,010416666

a)    : On calcul d’abord la mensualité de remboursement :

200 000 = a 1 – 1,010416666^-180 → a = 2 465,04 dh

                       0,010416666

         Il reste 96 mensualités à payer :

                            D84 = 2 465,04 1 – 1,0083333^-96 = 162 450,08 dh

                                                        0,008333

         Quand le taux diminue la valeur actuelle augmente, ici le client doit supporter une pénalité de 2,5 points (le taux annuel passe de 12,5% à 10% seulement).